РЕШУ ЦТ — математика

Задания

Задание № 27 Добавить в вариант

Сложность: IV

Классификатор алгебры: 6\.6\. Тригонометрические уравнения, решаемые разложением на множители

Методы алгебры: Группировка, разложение на множители

Методы тригонометрии: Использование основного тригонометрического тождества и следствий из него, Формулы кратных углов

Тригонометрические уравнения

Найдите (в градусах) сумму корней уравнения 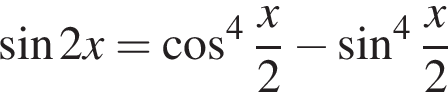$синус 2x= косинус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби минус синус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби$ на промежутке [−223°; 333°].

Решение. Заметим, что

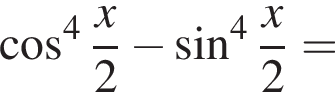
$косинус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби минус синус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби =$
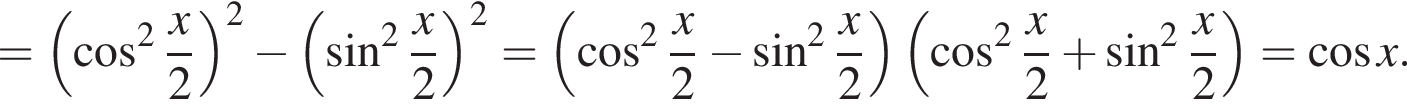
$= левая круглая скобка косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби правая круглая скобка в квадрате минус левая круглая скобка синус в квадрате { дробь: числитель: x, знаменатель: 2 конец дроби правая круглая скобка в квадрате = левая круглая скобка косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби минус синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби правая круглая скобка левая круглая скобка косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби плюс синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби правая круглая скобка = косинус x.$

Тогда имеем:

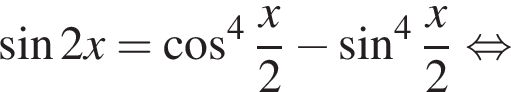
$синус 2x= косинус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби минус синус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби равносильно$
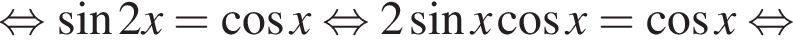
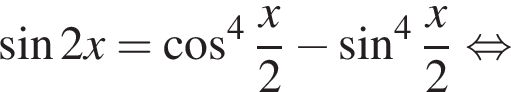
$равносильно синус 2x= косинус x равносильно 2 синус x косинус x= косинус x равносильно$ $синус 2x= косинус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби минус синус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби равносильно$
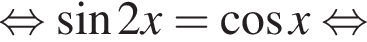
$равносильно синус 2x= косинус x равносильно$
$равносильно 2 синус x косинус x= косинус x равносильно$

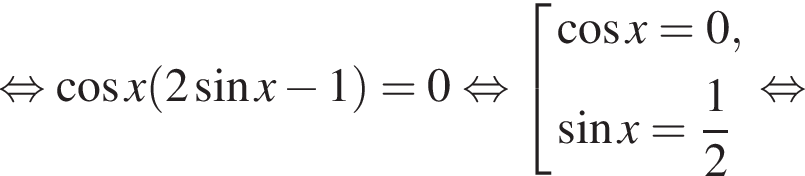
$равносильно косинус x левая круглая скобка 2 синус x минус 1 правая круглая скобка =0 равносильно совокупность выражений косинус x=0, синус x= дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . равносильно$
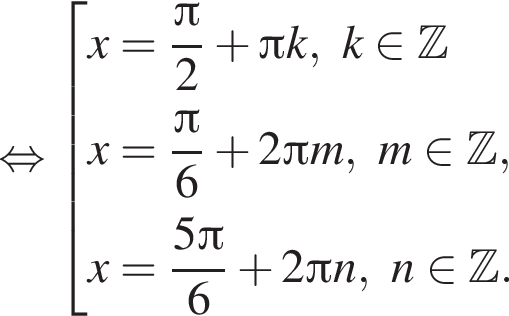
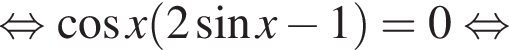
$равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k, k принадлежит Z x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи m, m принадлежит Z ,x= дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи n, n принадлежит Z . конец совокупности .$ $равносильно косинус x левая круглая скобка 2 синус x минус 1 правая круглая скобка =0 равносильно$
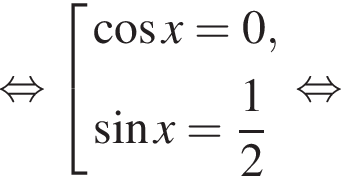
$равносильно совокупность выражений косинус x=0, синус x= дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . равносильно$
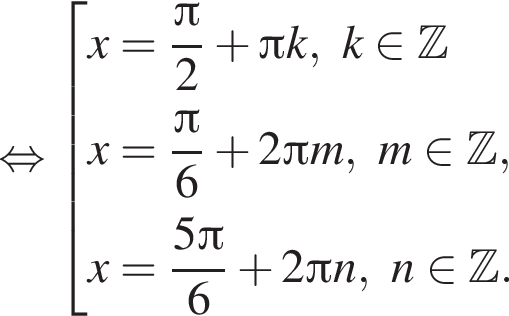
$равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k, k принадлежит Z x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи m, m принадлежит Z ,x= дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи n, n принадлежит Z . конец совокупности .$

На промежутке [−223°; 333°] лежат следующие корни из первой серии: 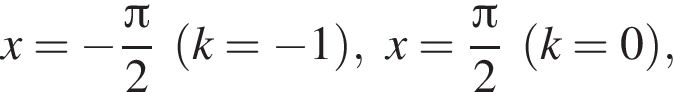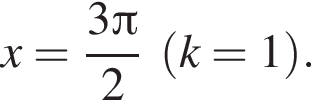$x= минус дробь: числитель: Пи , знаменатель: 2 конец дроби левая круглая скобка k= минус 1 правая круглая скобка , x= дробь: числитель: Пи , знаменатель: 2 конец дроби левая круглая скобка k=0 правая круглая скобка ,$ $x= дробь: числитель: 3 Пи , знаменатель: 2 конец дроби левая круглая скобка k=1 правая круглая скобка .$ Их сумма равна $дробь: числитель: 3 Пи , знаменатель: 2 конец дроби .$

На промежутке [−223°; 333°] лежат следующие корни из второй серии: 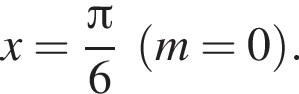$x= дробь: числитель: Пи , знаменатель: 6 конец дроби левая круглая скобка m=0 правая круглая скобка .$ Их сумма равна $дробь: числитель: Пи , знаменатель: 6 конец дроби .$

На промежутке [−223°; 333°] лежат следующие корни из третьей серии: 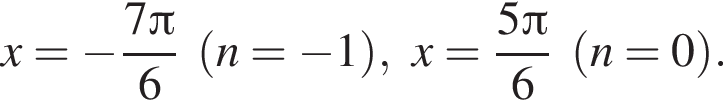$x= минус дробь: числитель: 7 Пи , знаменатель: 6 конец дроби левая круглая скобка n= минус 1 правая круглая скобка , x= дробь: числитель: 5 Пи , знаменатель: 6 конец дроби левая круглая скобка n=0 правая круглая скобка .$ Их сумма равна $минус дробь: числитель: Пи , знаменатель: 3 конец дроби .$

Поэтому сумма равна: 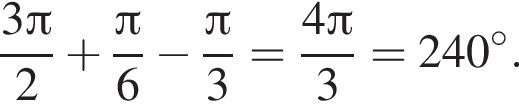$дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс дробь: числитель: Пи , знаменатель: 6 конец дроби минус дробь: числитель: Пи , знаменатель: 3 конец дроби = дробь: числитель: 4 Пи , знаменатель: 3 конец дроби =240 градусов.$

Ответ: 240.

Ответ: 240

240

Сложность: IV

Классификатор алгебры: 6\.6\. Тригонометрические уравнения, решаемые разложением на множители

Методы алгебры: Группировка, разложение на множители

Ключ

№ п/п	№ задания	Ответ
1	27	240